8.1 INTRODUCTION

Thus far we have been considering, under conveniently simplified assumptions, the location of individual units and also the location patterns of classes of similar units, or activities. It is now time to advance from such basic location theory into the domain of regional economics by focusing on two extremely important kinds of complexes of locational units and activities: the urban place and the region. This chapter deals with urban places and the next chapter with regions.

Some intimations of why and how cities¹ come into being have already emerged in the course of our inquiries into locational principles. In Chapter 3, reference was made to the special transfer advantages of large junctions and terminals, including intermodal transshipment points. In Chapter 5, we found that some types of activities favor a highly clustered pattern, in which certain external economies of agglomeration can be secured.

Thus if we define an urban place as a spatial concentration involving a variety of activities, we can already see some good economic reasons for the existence of such concentrations. The present chapter is addressed to questions of the size, spacing, and functional type of urban places. Here we shall be treating each such place as a single location.

There are two different (and basically complementary) approaches to an understanding of the location of cities. The first is historical: It asks why specific cities arose where they did, and why certain cities grew and others did not in a particular historical context.²  From this kind of case study we learn much about the diverse origins of individual cities. We find that for some, the decisive initial advantage of the site was its security against armed attack; for others, a good natural harbor convenient to a productive hinterland; for others, an easy place to cross a wide river or a mountain range; for still others, a pleasant climate or other amenities.

However, we also find that in many cases the original reason is no longer the principal basis of continued growth, and that once a city reaches substantial size it develops important economies of agglomeration that encourage still further growth.³  As Wilbur Thompson puts it, in his exposition of the urban size ratchet,

If the growth of an urban area persists long enough to raise the area to some critical size (a quarter of a million population?) structural characteristics, such as industrial diversification, political power, huge fixed investments, a rich local market, and a steady supply of industrial leadership may almost ensure its continued growth.⁴

The structural characteristics identified by Thompson are certainly important for the growth of an area. But the use of the term "ratchet" perhaps goes too far in implying that there is something irreversible about growth beyond the critical size. As we shall see later in this chapter, plenty of exceptions appear in recent data.

The complementary approach seeks to explain not individual cities and their peculiarities, but spatial distributions of cities as related to size and function. In developing a theory of "systems of cities," we first assume away all the special advantages of particular sites and imagine a uniform landscape—with all inputs equally available everywhere, demand for outputs evenly distributed, and transfer costs uniform in all directions, On such a tabula rasa, would economic forces give rise to some orderly pattern of urban concentrations? If so, what would it look like? The basic principles of urbanization patterns, disclosed by this kind of highly simplified analysis, can then be appropriately developed and modified to provide some useful insights about the real world. This is the approach pioneered by Walter Christaller and August Lösch and subsequently developed by many economists and geographers, notably Brian Berry.⁵  It is often called central-place theory.

8.2 THE FORMATION OF A SYSTEM OF CITIES

8.2.1 Some Simplifying Assumptions

In order to highlight the basic factors that give rise to spatial patterns of cities, we shall start with the highly simplified central-place model conceived by Christaller and Lösch. There are only two activities in this model: one rural and one urban. The rural activity is an extensive land user, such as agriculture, having no significant economies of agglomeration. The urban activity is subject to substantial agglomeration economies (internal, external, or both), but it can use land intensively and requires a relatively insignificant amount of space. People engaged in each of the two activities require the output of the other activity.⁶  All land is of uniform quality, and transfer costs are proportional to straight-line distance in any direction. The extensive rural activity, and consequently the demand for the output of the urban activity, is uniformly distributed.

It will be noted that in this rudimentary economic system, there are only two location factors: transfer costs and agglomeration economies.

8.2.2 Shapes of Trading Areas

As we found in Chapter 4, a single seller located somewhere in a limitless plain uniformly seeded with customers would serve a circular market area, its radius being basically limited by transfer costs on the goods sold.⁷  Such a situation is represented in Figure 8-1. Panel (a) of that figure shows a seller with the spatial demand curve D_s. The seller has established the f.o.b. price of p₀and produces at the rate of output q₀, which is given by the intersection of marginal revenue (MR_s) and marginal cost (MC) .The seller’s average total costs of production are represented by the curve ATC. Panel (b) is simply a map showing the seller’s location at point A and its circular market area.

But if we now envisage the urban activity being taken up in more locations, the market areas of the various sellers will impinge on one another. Thus in panel (a) of Figure 8-2, we find that a new seller located at C has cut into the market area of the seller at A by drawing away customers in the shaded area. Because the original seller at A now has fewer customers, its demand curve will shift leftward, forcing it to establish a lower f.o.b. price and reducing its profits. The decrease in demand is shown in panel (b) of Figure 8-2 as the shift from D_s, to D’_s.. For simplicity the marginal cost curve and the marginal revenue curves associated with the spatial demand curves have been omitted in Figure 8-2.)

As long as there are opportunities for profitable establishment of more production centers, these areas will become more numerous. Eventually, as new sellers crowd into the market, the demand curve of each seller will have shifted to a position shown by D"_sin panel (b) of Figure 8-2, where it is tangent to the seller’s average total cost curve, ATC. The market areas are now so compressed that all excess or economic profits are eliminated. Each seller earns normal profits, just sufficient to keep it in business, and there is no incentive for any more sellers to enter the market.

What will this "equilibrium" pattern of centers and trade areas look like? If all parts of the market are served from one center or another, if all the centers have equal locational advantages, and if the transfer surface is uniform, the areas must be identical polygons bounded by straight lines—as was stated in Chapter 4. Only three symmetrical and uniform shapes of market area will fill the surface under these conditions: squares, hexagons, and equilateral triangles. Of these, the hexagon is the "most efficient" in the sense that it gives the smallest average distance between sellers and buyers.⁸  A honeycomb is a good example of how initially circular areas (cells) become hexagonal when pressure squeezes them into a shape that will utilize all the available space.

But in many cases the transport grid is basically rectilinear—as in most modern urban street patterns and over a major part of the rural area of the United States, where the land surveys were made in terms of a checkerboard of square townships and sections and where most local roads have followed section and township boundaries. Under such conditions, market-area boundaries and the trading areas of towns tend to be not hexagonal or triangular but square.

8.2.3 A Hierarchy of Trading Areas

Next, we shall take a more realistic approach by recognizing more than just a single urban activity. The size of the trade area for a specific product depends on (1) the nature of the spatial demand curve and (2) cost or supply considerations. From our discussion of the spatial demand curve and pricing in Chapter 4, we can isolate transfer costs (per ton-mile) and market density (per square mile) as the crucial demand factors determining the size of trading areas. On the supply side, the extent of scale or other agglomeration economies (as shown by the ATC curve) are most important. Obviously, each of these conditions varies from one activity to another. Accordingly, we might expect that each new urban activity we introduce will have a different appropriate size of market area and spacing of supply centers. The appropriate area will be small, and the centers closely spaced, for products for which there is little economy in agglomeration or for which the density of market demand is high. Where the contrary conditions hold (important agglomeration economies or sparse demand), we should expect production to be concentrated in a few widely spaced centers each serving a large area.⁹

But should we really expect to find as many different and independent systems of market areas and production centers as there are different products—an almost infinite variety? We might expect this were it not for the economic advantages of channelizing transfer along a limited number of efficient routes, and the advantages of clustering different activities in the same place so as to get the external economies of agglomeration discussed in Chapter 5. Recalling those considerations, we can see why two or more activities for which the "ideal" pattern of centers may be only slightly different are, in fact, likely to settle for a common "compromise" set of production locations. And if two activities do have very different ideal sizes of areas, the tendency is for the activity with the larger-sized areas to locate at some of the centers of the other activity—say every other one, or every third, fourth, or tenth one. In this way, each activity can have a pattern of centers more or less appropriately spaced to fit its conditions, while at the same time the total number of centers is kept down. This is an advantage because bigger centers provide more economies of agglomeration and because more of the total flow of goods and services can travel on efficient high-volume transfer routes.

The pressure for reduction of the number of size classes of areas is so basic that we might even embellish the vocabulary of regional economics by referring here to a Procrustean Law of market areas. Procrustes was a mythical innkeeper who provided only one bed for all his guests and achieved a perfect fit by stretching or cropping each guest as required.

What all this implies is a hierarchy of central places. As this sorting takes place and activities with larger-sized ideal areas locate at some of the centers of other activities, this results in some central places having a greater variety of goods. As the number of activities becomes large, we can envision some centers with a much more complete set of activities than other centers. A stylized example of such a system is shown in Figure 8-3. In this particular hierarchical pattern, it is assumed that the areas are square. Four "orders" or size classes of centers are represented by different sizes of dots, and their respective areas are bounded by black and gray lines (shown at the right of the figure).

There are many possible variations on this scheme; they have been analyzed in detail for both the square and the hexagonal systems and need not detain us here. However, one particular feature is important for an understanding of urban and regional structure. In the system of cities shown in Figure 8-3, each city of any but the smallest size class serves as the center not only for its area but also for an area of each of the smaller sizes. The implication is, in fact, that each order of centers carries on the activities of all lower orders of centers plus some further activities not found in such places. Thus even in the largest city, retail customers have the opportunity to buy goods and services found also in the smallest hamlet, but retail customers in smaller places inevitably must look to larger towns for some of their shopping needs.

As we shall see from some empirical evidence to be introduced later, the mix of activities in urban places of various sizes does in fact conform rather closely to what we should expect under a fully hierarchical organization of this sort. Larger centers do have most if not all of the kinds of urban activities found in smaller centers.

Another feature of the central-place hierarchy characterized in Figure 8-3 is that it exhibits a constant nesting factor (in this case, 2). That is, market-area size (i.e., the physical extent of the market) increases from one level of the hierarchy to the next by a constant factor, so that the number of market areas of one size class that nest into the next largest size class does not vary as one proceeds through the hierarchy. Central-place models need not have this attribute, although the hierarchy developed by Christaller did. John B. Parr has developed a more general system that allows for variability in the nesting factor.¹⁰  As a result, the ratio at which market-area size increases from one level of the hierarchy to the next may differ at each step up the ladder. This flexibility has the potential of contributing significantly to the descriptive power of central-place models.

The basic concept of a central-place hierarchy contributes importantly to our understanding of intraurban location patterns. In the preceding chapter, we identified the phenomenon of subcenters as an elementary characteristic of urban spatial structure. Having recognized the interurban hierarchy of central places, it is but a small extension to view the subcenters found within metropolitan areas as central places on a more micro level.¹¹  Corresponding to the central-place hierarchy of hamlet, convenience center, shopping center, and wholesale-retail center in terms of urban places, we have an intraurban subcenter hierarchy of streetcorner, neighborhood, and community center with progressively greater size, variety, and market area.

8.2.4 Some Practical limitations

The highly simplified central-place model presented so far provides a rationale for patterns of cities such as the one shown in Figure 8-3. There are many size classes of cities; each larger class has a more comprehensive array of urban activities and comprises a smaller number of cities spaced farther apart. We should expect the various extensive rural activities (for example, distinctive types of agriculture) to be arranged in concentric zones around the centers, in the manner shown in Figure 6-4. Any given city above the lowest order will have more than one rural market area (for its various outputs) and more than one rural supply area (for its various rurally produced inputs); there is no reason to expect any of its market areas to coincide with any of its supply areas. In addition, all cities except those in the largest class may be getting urban products from cities of larger size.

This is obviously not an adequate picture of cities, areas, and trade flows in the real world. We begin now to consider some of the additional factors involved.

First, the simple model assumed a uniform transfer cost per mile on a fine and regular grid of routes, and also assumed that the rural market was distributed with uniform density. Recognition of a less regular transfer network, with some routes cheaper or better than others, and recognition of variations in the density of demand, would lead us to expect substantial deformation of the areas and city patterns. Still further deformation arises because the costs of inputs and the resulting costs of production are not really the same in different cities, even among those of the same size class. The many activities that are sensitive to location factors other than agglomeration economies and access to markets were ignored in the simple model; superimposing their locations on the basic central-place scheme further complicates the pattern, creating additional cities (and! or larger cities) by adding both more urban activity and more demand. Finally, the whole pattern of locations is constantly shifting in delayed response to changes in such conditions as population, regional income levels, transfer costs, and technology, so that no picture of an equilibrium situation can be realistic.

These practical considerations are ample to explain why the distribution of cities by size is not stepwise by discrete hierarchical classes but continuous;¹² and also why there are only loose relations between the population of a city and the size of its trading area, and between city size and the range of activities represented in a city.

8.2.5 Generalized Areas of Urban Influence

Although the central-place model described implies that any city above the smallest class has a variety of different-sized market and supply areas, people frequently refer to "the" trading area (or tributary area, or area of dominance) of a city, as if there were only one. The identification of appropriate and useful nodal regions, which will be taken up later, relies heavily on the notion that for a considerable range of purposes (though perhaps not for all purposes) we can mark out some single area as particularly related to a given center.

For example, in one of the early studies of spatial trading patterns by marketing specialist William J. Reilly, an attempt was made to induce an empirical formula to explain retail trading areas of cities in terms of their size.¹³  Reilly's Law of Retail Gravitation says that "two cities attract retail trade from any intermediate city or town in the vicinity of the breaking point [the boundary between their spheres of dominance], approximately in direct proportion to the populations of the two cities and in inverse proportion to the squares of the distance from these two cities to the intermediate town."¹⁴

Some overlap of market areas is recognized, but according to this law, the market-area boundary in the sense of the "breaking point" (where trade is equally distributed between the two supplying cities) runs through points where

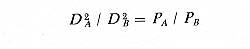
if P_Aand P_B are the respective populations of the two cities A and B, and D_A and D_B are their respective distances from the boundary. This means that if A and B are of equal size, the market-area boundary is a straight line midway between them; but if, for example, A is twice as large as B, each point on the market-area boundary is times as far from A as from B. Figure 8-4 shows a hypothetical set of four centers and their areas.¹⁵  Reilly’s Law worked reasonably well when tested against actual situations (which might be expected since it was derived empirically rather than theoretically) and has proved more durable than many other "laws." Let us see how it might be rationalized in terms of the simple central-place model by making the situation a little more realistic.

Consider a rural family living midway between a small town and a somewhat larger town. If they want to buy gasoline or a loaf of bread, there will be no particular reason to prefer one town to the other, and shopping trips wholly devoted to such "convenience purchases" would tend to be about equally divided. If the trip is to include going to a movie or buying a suit of clothes, however, the preference would be for the larger town, since its clothing stores have a wider selection and it may have two movie theaters compared to one in the smaller town. Trips of this sort, then, will be directed predominantly to the larger shopping center. Finally, there are some things (perhaps binoculars, or parts for the washing machine) that cannot be purchased at all in the smaller town but are available in the larger one. Any shopping trip including such an errand will have to be directed to the larger town.

The relative populations of the four towns, A,B,C, and D are as indicated in parentheses. A’s trading area includes all territory outside the circles. All boundaries consist of circular arcs.

For obvious reasons of economy of time and money, people try to consolidate their errands and perform multipurpose trips. It is clear, then, that the majority of trips for this family located at the half-way point will be in the direction of the larger town because of the greater range of its activities. To find a family that splits its trips evenly between the two towns (that is, to locate the trading-area boundary) we would have to go some distance down the road toward the smaller town.

8.3 TRADE CENTERS IN AN AMERICAN REGION-THE UPPER MIDWEST STUDY

The applicability and relevance of the central-place approach is brought out in a study made in the mid-1960s of urban places in the Upper Midwest, a large area defined for purposes of the study as coterminous with the Ninth Federal Reserve District. This study was part of a much larger project analyzing economic activity and trends in the area.¹⁶

The purpose of this investigation was to provide some guidance to planning and development activities involving cities and towns in the Upper Midwest region. No attempt was made to predict growth or recommend development policies for any specific urban place. But as a basis for any subsequent efforts with such local application, the study developed some interesting and useful findings regarding the characteristics and growth trends of categories of places, corresponding conceptually to the "orders" of the theoretical central-place hierarchy.

The first step was a listing of retail and wholesale activities, arranged according to the smallest size of community in which they are consistently represented. Figure 8-5 shows this grouping and the way in which it was applied in classifying the individual trade centers. Thus in order to rank as a "minimum convenience" center, a place had to have all of the last six activities shown, and at least two of the preceding four (garage, auto, implement dealer; variety store; meat, fish, fruit; general merchandise). To qualify for the highest rank,¹⁷ a trade center had to have every one of the activities listed. The category of "hamlet" was added as the lowest order of trading center. In general, hamlets contained a gasoline station and an eating place but no consistent set of further trade activities.

In all, more than 2200 centers were thus classified (see maps, Figure 8-6eand Figure 8-6w). Table 8-1 shows the numbers and sizes by hierarchy level. It will be observed that the higher orders of centers are progressively fewer and larger; but there is much overlapping of size ranges, reflecting the fact that a center’s trading activity is not the sole determinant of its employment or population.

The study explicitly recognized that each type of center higher than a hamlet has more than one size of trade area.¹⁸  The method used to determine the trade areas of the highest orders of centers (primary and secondary wholesale-retail) was based on relative frequency of telephone calls. From shopping and convenience centers within its area, a "wholesale-retail center" received more calls than any other center at its own level, and at least half as many calls as any "metropolitan center."¹⁹

Trade areas at the "complete shopping" level were "defined by lines drawn at highway half-distances between complete shopping centers, then adjusted for barriers, such as mountain ranges, and differences in sizes of competing centers."²⁰ It is interesting to note in Figure 8-6eand Figure 8-6w that these areas are larger (that is, the complete shopping centers are spaced farther apart) in the western and extreme northeastern parts of the Upper Midwest, where the density of population and income per square mile is less. This is in accord with the theoretical expectation indicated earlier: Trade-area size is inversely related to market density.

Figure 8-7 shows the much larger trade areas at the "secondary wholesale-retail" level. Here again, the areas are more extensive where population is sparser, and there is an observable tendency for the areas to be asymmetrical, extending farther in the direction away from metropolitan centers. This same asymmetry was noted as a theoretical expectation in Figure 8-4, but there is an additional reason for it. A large part of the goods distributed from the wholesaling centers are bought from manufacturers or large distributors in the metropolitan centers and other places outside the region, and transfer costs make their prices higher as we go farther from those sources. Consequently, a trade center in the Upper Midwest can compete more effectively with other centers of its own rank located farther from the sources of the goods than it can with competing centers located closer to the sources.

Trade and service areas of metropolitan centers serving the Upper Midwest are shown in Figure 8-8. This demarcation of areas was based on relative frequencies of telephone calls received from wholesale-retail centers, and the progression of frequencies is mapped for Minneapolis, St. Paul. It will be observed that the number of calls (per 100 inhabitants at the wholesale-retail centers where the calls originate) first falls off very rapidly and then more and more gradually with increasing distance from the metropolitan center.

8.4 ACTIVITIES EXTRANEOUS TO THE CENTRAL—PLACE HIERARCHY

Let us now consider more explicitly some of the limitations of the simple central-place model. So far in this chapter, our assumption has been that both markets and sources of transferable inputs for urban activities are uniformly distributed in space. The resultant theoretical patterns of market areas and central places simply reflected the locational effects of the economies of agglomeration available to various kinds of urban activities. We have as yet no rationale for any flows of goods or services (other than primary rural products) either "up" the steps of the urban hierarchy or "horizontally" among cities of equal status. Yet in reality, enormous flows of these types occur. Clevelanders buy cigarettes from Durham, North Carolina, automobile tires from Akron, frozen orange juice made in small towns in Florida, and government services from Washington, D.C., and Columbus, Ohio. How does all this relate, if at all, to the hierarchical scheme of urban places, activities, and market areas?

The clue is that neither markets nor transferable inputs are uniformly distributed. Although for most kinds of consumer goods and services there is a market wherever people live, there are some consumer goods and services that are used mainly or exclusively by people in certain regions, by people in larger cities, or by rural and small-town people. For inputs, the lack of ubiquity is even more pervasive. Labor supply, of a sort, exists wherever people live; but other inputs—such as specific crops, minerals, manufactured goods, or services—are found only in certain places, and with wide variation in both cost and quality.

Let us consider the locational implications. We can usefully distinguish three classes of activities according to whether their locations are (1) predominantly in larger cities, (2) predominantly in small cities or towns, or (3) not associated with any particular size of city. (Certain manufacturing industries are cited as examples in Appendix 8-2.)

Those activities dependent on the external economies of urban concentration are predominantly located in large cities. This class of activities has already been discussed in Chapter 5. Their outputs are disposed of in the cities where produced, in other cities of all sizes, and in rural areas as well. In other words, the flow is mainly downward in the hierarchy, but it is also horizontal at the highest levels. Activities of this type fit reasonably well into the hierarchical central-place scheme.

There are several reasons why an activity might be found mainly in small centers. First, this is the normal location pattern for processing operations strongly oriented to rural inputs or to other inputs derived from extensive land uses; these uses tend to be crowded out from highly urbanized regions by more intensive claimants for land. Forestry and grazing are such activities: Sawmills and meat-packing plants are most often not located in large cities, because they must be close to types of land use usually associated with sparse settlement. Meat packing would be even more a small-town industry were it not for the practice of shipping cattle from range lands to fattening areas prior to slaughter.²¹  The processing of perishable crops is so strongly input-oriented that individual plants have quite small supply areas; and simply on a probability basis, very few of those areas will contain a large city.²²

Small-town locations are characteristic for activities associated with extensive outdoor recreation. These activities need plenty of space, and in some cases (such as ski resorts) topographical or climatic conditions not typical of large cities.

Finally, small cities and towns usually provide lower living costs and wage levels. Thus activities strongly oriented to cheap labor as such, and footloose with regard to other locational considerations, are likely to prefer the smallest size place that will provide enough workers for a plant of efficient scale. Most American textile mills, and a wide variety of industries making fairly standardized apparel items (such as shoes), are now found in rather small cities and towns, the principal explanation being labor-cost economies (Chapter 10 gives further attention to the origins and effects of labor-cost differentials).

There are even some basically clerical activities for which a small-town location is appropriate for serving a nationwide market, since labor and space are cheap, and the inputs and outputs move by mail. For example, the U.S. Bureau of the Census maintains its central office for the searching of Census files to establish birth records for individuals at Pittsburg, Kansas. One of the larger life insurance companies maintains its central office at the very small city of Montpelier, Vermont. Most other firms in this field, however, are in larger cities. For activities located in small cities, the flow of outputs is mainly up the urban hierarchy to markets in larger cities; but it is also partly horizontal, since only some but not all small places have the activity in question.

There are a large variety of activities for which size of city seems essentially irrelevant. They occur indiscriminately in small, middle-sized, and large cities. Some of these are primarily oriented to a localized natural advantage such as water (for processing or for transport) or a mineral resource, and their agglomeration economies are internal, involving merely the scale of the individual unit. Thus salt mining and processing works are found both in isolated locations and within the city of Detroit; steelworks are found both in large cities such as Chicago and in quite small cities such as Butler, Pennsylvania, or Provo, Utah; and automobile parts, electrical equipment, furniture, whiskey, candy, and many other manufactured goods are made in locations seemingly selected without any systematic concern for city size. There is no discernible relationship here to the hierarchical scheme of central places in terms of market areas, industry distribution patterns, or the flow of inputs or outputs.

In view of such kinds of activity that do not seem to fit the hierarchical central-place scheme at all, we can readily understand why the relation of range of commercial functions to size of trade area and to city size is less than exact. In fact, it may be surprising that there is as much evidence of hierarchical regularity as does appear. Let us take another look at the principles involved.

The relationship between trade-area size (that is, spacing of cities) and urban functions principally involves retail and wholesale trade, which were in fact the basis of the hierarchical ranking in the Upper Midwest investigation. Some kinds of manufacturing also play a similar role. Bakeries, soft drink bottling plants, sheet metal shops, ice cream plants, job printing and newspaper plants, and many other industries can be arranged in a reasonable sequence according to the minimum size of market required, in the same way that different lines of trade or services are, and it is possible to identify roughly the threshold size of place above which each is likely to be found. Many kinds of services (shoe repairing, movies, bowling alleys, doctors, lawyers, hospitals, realtors, morticians, broadcasting stations, and so on) can likewise be more or less appropriately fitted into the central-place order. Moreover, something very like the trade center hierarchy appears in the public services provided in the hierarchy of unincorporated settlements, villages, towns, county seats, and state capitals.

But many urban places, at all size levels, also contain what we can call noncentral-place activities. Consider, for example, a small town whose retail trading area extends only a dozen miles, but which now acquires a shoe factory serving a wide regional or even a national market. That town now has a large employment and population compared to either the size or the population of its rural trading area. In this respect, it has been put out of line with the hierarchical scheme. But we must recognize that its trading area includes itself. The town needs grocery stores, drug stores, and the like to serve the shoe factory employees as well as the rural customers and the people employed in central-place activities. Both the amount and the variety of its central-place business will become greater than they were before the shoe factory came. Thus the town will occupy a higher rank in the hierarchy. Finally, by virtue of the wider range of available goods, we can expect the town to draw rural customers from a larger area than before, at the expense of rival towns not blessed by new factories. (Some of those towns may as a result lose previous retail functions and sink in the hierarchy.) The ultimate equilibrium situation may turn out to be reasonably close, after all, to what the central-place formulas would suggest in terms of the relation between town size, range of central-place activities, and size of trade area.

This example shows that there may be a good deal more relevance in the theoretical central-place relationships than one might infer, in view of the fact that so many activities (like the shoe factory in this example) are located extraneously. It is no longer quite so surprising that we find the degree of hierarchical regularity that does appear in the real world. We can see also how individual towns and cities can break out of their positions in the hierarchy and either rise or fall. The system, even in theory, has internal mobility.

8.5 TRENDS IN URBAN PATTERNS

In later chapters we shall be considering some of the reasons why certain cities and regions grow faster than others and what some of the major observable trends of change are. We now consider briefly how the central-place model can throw some light on changes in the relative importance of cities of different orders of size.

The Upper Midwest study and other studies brought to light a tendency for the smaller trade centers to grow more slowly than the middle-sized and large ones, and it is clear that a great many hamlets and villages have actually disappeared. Table 8-2 provides some evidence of this trend.

There is some tendency for population growth of a place to be directly related to its size, and hence to its previous growth. This is to be expected throughout the main agricultural regions of the Upper Midwest since the chief functions of most communities are trade, service, and agricultural processing. The past thirty years’ change in these areas has been characterized by adjustment to modern transport and modern agricultural methods. Although farm population in the trade areas of these cities has declined, the value of agricultural production has been sustained or increased. The changes that have taken place have involved mainly consolidation and centralization of many business functions and, hence, employment opportunities. In general, the larger a place was at the beginning of the automotive era, the better have been its chances to retain old functions and acquire new ones.²³

In this respect, the experience of the Upper Midwest region is representative of that of the United States as a whole. Throughout much of this century, population growth in metropolitan areas exceeded that of nonmetropolitan areas. During the 1970s, however, there was a reversal of this growth pattern.

Table 8-3 shows this turnaround. During the 1960s, the population in metropolitan areas increased by 17 percent, while the increase in nonmetropolitan areas was only 4 percent. Since 1970, metropolitan area growth has been only 9.5 percent, compared with nonmetropolitan growth of 15 percent and national population growth of approximately 11 percent.

The United States remains a largely metropolitan nation, with 1980 population figures indicating that 73 percent of the total population is metropolitan (165.2 million in a total population of 225.5 million). However, the contribution of metropolitan areas to the national population increase has changed substantially. During the 1970s, the nation’s population increased by 22.2 million. Of this increase, only 14.3 million, or roughly two-thirds, occurred in metropolitan areas. By comparison, 92 percent of the nation’s growth was accounted for by the same metropolitan areas during the 1960s.

We observe also in Table 8-3 that the percentage increase in population growth for the largest metropolitan areas is substantially less than that for other metropolitan areas during the 1970s. Again, this reverses a pattern that had prevailed through the 1960s. Several of the nation’s largest metropolitan areas—including New York, Boston, Philadelphia, Buffalo, Pittsburgh, Cleveland, Detroit, Milwaukee, and St. Louis—had declining population during the 1970s. Of these, only Pittsburgh had lost population during the 1960s.²⁴

The abruptness of the turnaround as reflected in these figures is to some extent deceptive. William Alonso has observed that the demographic forces affecting population changes in metropolitan areas began to take shape well before 1970.

By the 1960s ... the migration rate into metropolitan areas was small, and three-fourths of metropolitan population growth was based on natural increase, and only one-ninth on migration from nonmetropolitan areas, the balance resulting from immigration from abroad. Now the decline in the rate of natural increase has cut the growth rate sharply, and this has been accented by the reversal of net migration into nonmetropolitan areas. ²⁵

Thus it seems that the decline in the population’s natural rate of increase (defined as the birth rate minus the death rate) has merely exposed some long-standing economic forces governing migration patterns.²⁶

Table 8-4 offers additional insight on the character of nonmetropolitan growth. Here the nonmetropolitan population is classified as residing in incorporated places of different size classes and in unincorporated areas. We find that the inverse relationship between the size of the population in a place and its growth, so characteristic of metropolitan areas in the 1970s, extends to very small incorporated areas. However, the percentage increase in population of these places is modest when compared to the percentage increase in population for the nation as a whole over this period, which was approximately 11 percent (as shown in Table 8-3). Table 8-4 shows that only settlements with 1980 populations below 2500 grew faster than the national average. In contrast, the population growth outside of incorporated cities, towns, and villages has been substantial. Thus nonmetropolitan growth in recent years is not simply urban growth on a small scale.

In some instances, the population trends described above reflect changes that have occurred within the central-place hierarchy. In others, changes that are largely extraneous to that hierarchy have been most important. In either case, however, the effects of these changes are transmitted throughout the central-place system. We therefore turn to this model for some perspective on these developments.

Trends of the sort documented above may result from a tendency for many specific central-place activities to assume a more concentrated or a more dispersed pattern (i.e., abandoning smaller places in favor of larger ones or the reverse) because of changes in the basic conditions determining their efficient scale and degree of dispersion. These conditions we have identified as (1) the density of demand for their outputs, (2) the degree to which they are subject to scale or other agglomeration economies, and (3) the level of transfer costs on their outputs.²⁷

Increased density of demand makes it possible for the activity to sustain itself with smaller trade areas; by the same token, when demand density declines, fewer centers and areas can survive. In many agricultural sections of the Upper Midwest and elsewhere, the farm population has been thinning out for several decades because of the trend toward larger and more mechanized farms employing fewer people on any given area. The American farm population has been shrinking rather steadily for nearly half a century. While the rate of decline slowed somewhat during the 1970s, the long-term downward trend has persisted,²⁸  and the increases in nonmetropolitan population that took place during the 1970s were almost entirely in nonfarm areas.²⁹  In many areas, of course, per capita farm income rose more than enough to compensate; but it is reasonable to surmise that a smaller number of farmers, even without a drop in their aggregate real income, represents a reduced demand for the kinds of goods and services available in the smallest settlements. At the same time, there has been a tendency for more farmers to live in town and commute to their farms, or to move to town in the winter. Consequently, farm population trends appear to provide some of the explanation for the slow growth or decline of the smallest trade centers prior to 1970.

The recent growth in nonmetropolitan populations also has implied shifts in the density of demand. Table 8-3 indicates that suburban development beyond officially recognized metropolitan-area boundaries accounts for some nonmetropolitan growth, both in the 1960s and in the 1970s. In each decade, nonmetropolitan counties closest to urban centers (those with 30 percent or more commuting) had large percentage changes in population. Estimates by the Bureau of the Census suggest that one-fourth to one-third of nonmetropolitan growth can be attributed to this outer suburban or "exurban" development.³⁰

This is not the only source of increased density of demand in smaller central places, however. Counties that had high concentrations of retirees in 1970 also had substantial population growth in the decade to follow.³¹  The importance of this phenomenon for some nonmetropolitan areas is obvious (as in many parts of Florida and Arizona, for example), but its significance is much more general. An extensive analysis by Kevin F. McCarthy and Peter A. Morrison of population growth rates by counties in 26 states during the first half of the 1970s shows sharp gains in growth rates for areas that they classify as specializing in retirement, particularly in rural and less urban areas.³²  They also find that nonmetropolitan counties specializing in recreation posted similarly impressive gains. It appears that these amenity-rich areas may be a major beneficiary of higher levels of national income and increases in leisure time.

Increased economies of scale for an activity have the effect of enlarging trade areas and concentrating the activity in fewer and larger urban centers. Scale economies have not been as conspicuously enhanced in trade activities as in industrial activities; but the modern supermarket and shopping center have developed mainly within the past generation and constitute a major change. We must also reckon with the fact that higher living standards make consumers more sensitive to the appeals of variety in shopping goods and hence add to the competitive advantages of larger trading centers that can provide such a variety. Recognition of scale economies has been evidenced also in the trend toward consolidation and concentration of many public activities, such as schools and health services. Thus on the whole, this factor has probably contributed to faster growth of middle-sized and larger trade centers at the expense of smaller ones.

The spread of good roads and automobile ownership has, of course, enabled rural and small-town people to make longer shopping, crop-delivery, and other trips, and this factor also should be recognized as part of the explanation for the observed trends of urban growth. But the effect of changes in the level of transfer costs on trade-area size and on the spacing of trading centers is less straightforward than it might appear.

If transfer were assumed to be altogether costless, urban activities could be concentrated at the points of lowest operating cost, and economies of agglomeration would tend to concentrate all of an activity in one place. At the other extreme, if transfer were infinitely costly (that is, impossible), each location would have to be self-sufficient. From this contrast of extremes, we might infer that cheaper transfer always enlarges trade areas and leads to fewer, larger, and more widely spaced central places. A similar inference could be drawn by regarding transfer services and the services of factors of production as complementary inputs, with possibilities of substituting a cheaper input for a more expensive one. Then if transfer services became cheaper, we should expect that more transfer would be used in relation to output: that is, distances between seller and buyer would increase and trading areas would be larger. This is what we may call the substitution effect of a change in transfer cost.

This simple formulation, however, overlooks some side effects of changes in the level of transfer cost. First, there is what might be called the income effect of such changes. If transfer becomes cheaper, buyers at any distance from the trade center will get the goods cheaper and will normally buy more. With greater sales per buyer, a smaller trade area will suffice to provide the scale economies needed to sustain a center. More centers will be able to survive. The income effect of a reduction in transfer costs, then, is a reduction in trade-area size, and it is similar to the effect of an increase in demand density (that is, population density, per capita income, or both).³³

There is another way, too, in which cheaper transport may tend to reduce the size of trading areas and lead to a more dispersed pattern of centers. The degree to which activity is concentrated in locations of low operating cost depends on (1) transfer costs and (2) the magnitude of the differentials in operating cost. If transfer becomes cheaper while the operating cost differentials remain the same, urban activity will become less transfer-oriented and will tend to cluster more in efficient operating locations. But in fact, reduced transfer costs are likely to narrow the operating cost differentials, insofar as they enhance the mobility of labor and other production factor inputs. Here again, a change in the level of transfer cost cuts both ways in regard to agglomeration versus dispersion, and the net effect could be in either direction.³⁴

Changes in the basic conditions determining the efficient scale and dispersion of activities—such as those conditions discussed above—are not the only reason for the changes we observe in the urban place pattern. The structure of the hierarchy is affected also by changes in the mix of activities. It has been mentioned already that, as a result of higher levels of income and leisure, consumer demand tends to shift from staple necessities to a wider range of shopping goods and luxuries, with variety becoming a more important dimension of competitive advantage for producers. While this clearly favors the large trade center, we must also recognize that the national economy is becoming much more dependent on service activities and much less dependent on manufacturing per Se. As population in nonmetropolitan areas increases, the growth of services will follow, since services are highly oriented toward their respective markets. This fact is surely reflected in the population growth associated with nonmetropolitan areas having high concentrations of retirees or specializing in recreation that were noted above.

The framework of the central-place model is relevant in assessing some of the factors governing trends in urban patterns. However, a number of trends in noncentral-place activities must also be considered. Generally, as the economy develops, a greater proportion of productive activities involves later stages of processing and handling, and a smaller proportion uses rural products directly as inputs. Fewer and fewer activities need to be oriented closely to inputs from rural extractive activity (as do canneries or sawmills); in contrast, there is the widening range of activities (such as the production of electrical equipment, pharmaceuticals, or books) that are technologically remote from any extractive process. Accordingly, there is less and less reason for many activities to be located in small settlements for the sake of easy access to agricultural, forest, or mineral products. Finally, the increasing variety and complexity of goods, services, and productive operations in general calls for more close inter-firm and interactivity contact, and tends to increase the locational importance of urban external economies of agglomeration.

Until very recently, each of these factors contributed to the advantages held by larger metropolitan areas for manufacturing activity. However, technological advances in production have begun to alter this pattern. Considerable simplification has occurred in some production processes that had involved the acquisition of mechanical components in order to assemble machines or other goods. Developments in electronics have contributed to this trend and have changed interindustry relations significantly. Now, one printed circuit or microchip may substitute effectively for numerous other parts. As the importance of these "high-technology" goods has increased, the bond of agglomeration economies that had so strongly influenced location patterns has loosened; proximity to a wide array of parts suppliers is no longer essential. These modern components are easily transported, thus freeing both the producer of high-technology goods and the industrial user to evaluate a wider range of location alternatives. For some, this has meant taking advantage of relatively low wages and living costs in nonmetropolitan areas. As discussed in Chapter 3, improvements in information storage, retrieval, and transmission facilitate such choices.³⁵

While one might portray this as a technological change in one activity (electronics) that has affected other activities in an exogenous way, some researchers see it as part of a larger endogenous process in the life cycle of many different manufactured goods. They argue that over time, the standardization of production processes takes place. Once this occurs, decentralization of activities can be expected, since they are no longer tied by agglomeration economies to large urban complexes. In this analysis, the diffusion of technology to more peripheral areas also enhances the potential for innovation in these regions at the expense of innovation potential in older industrial centers, thus promoting further decentralization.³⁶

8.6 SUMMARY

Central-place theory attempts to explain the spatial patterns of trade and service centers. According to this line of analysis, centers for the distribution of some single good or service to users scattered uniformly over an area would develop at equidistant sites. Their market areas would all be of a uniform size determined by transfer costs on the output, density of demand per unit area, and scale economies in the production and/or marketing of the output.

These market-area determinants would ideally call for a different uniform size of trading areas, and a finer or coarser scatter of distribution centers or central places, for each kind of output. But because of external economies of agglomeration and the economies of channeling transfer along high-volume routes, many different kinds of trade are conducted in a single central place; and instead of a separate set of centers to handle each product, there is evolved a rough hierarchy of central places. Central places range from very small and simple ones carrying on only one or two lines of highly local trade, through higher classes of central places progressively larger, more widely separated, and having more different lines of trade and sizes of trading areas. In the hierarchy, each size class of places carries on all the trading activities practiced in all lower size classes, plus some further types of activity not found in any smaller centers.

The spatial, functional, and size distributions of trading centers in the real world, as identified in such empirical investigations as the Upper Midwest Economic Study, conform only roughly to the simplified ideal central-place model, because many additional location factors affect the growth of specific activities in specific centers, and neither transfer costs nor demand densities are actually uniform. Such studies are, however, useful in assessing the changing roles of urban centers of various size classes and trading functions in a regional economy when population, income, and transfer and other technologies change. In the United States, trends toward concentration of more trading activities in larger centers, lengthening of the retail buyer’s journey, and relative decay of many of the smallest settlements can be logically explained in terms of a central-place model.

The trading areas of larger centers are enlarged by the attraction that variety holds for shoppers and the fact that people often combine purchases of different types on a single trip. A larger center has also some lines of trade in which trading-area radii are characteristically larger than those of the businesses found in smaller places. An empirical measurement of this size relation was stated in Reilly’s Law, a gravity formulation that makes a center’s trading-area radius proportional to the square root of its population.

The assumptions of central-place theory are clearly inapplicable to many urban activities (including most kinds of manufacturing). Some of those activities appear to locate without regard to city size. It is possible, however, to identify empirically certain groups of activities that are relatively concentrated in specific size classes of cities and to explain such concentration patterns in terms of considerations complementary to the central-place model.

The United States has experienced major changes in the relative importance of cities of different orders of size. With the 1970s came the reversal of a long-standing trend toward greater growth rates in larger metropolitan areas. Explanations of these developments lie within the central-place framework as well as beyond it. Regardless of the source of these changes, however, the effects are distributed throughout the urban hierarchy.

SELECTED READINGS

Martin Beckmann, Location Theory (New York: Random House, 1968), Chapter 5.

Dennis R. Capozza and Kazem Attaran, "Pricing in Urban Areas Under Free Entry," Journal of Regional Science, 16, 2 (August 1976), 167-182.

M. L. Greenhut and H. Ohta, Theory of Spatial Pricing and Market Areas (Durham, N.C.: Duke University Press, 1975).

Edgar M. Hoover, "Transport Costs and the Spacing of Central Places,"Papers of the Regional Science Association, 25 (1970), 255-274.

Charles L. Leven (ed.), The Mature Metropolis (Lexington, Mass.: Lexington Books, D. C. Heath, 1978), pp. 23-41.

August Lösch, Die räumliche Ordnung der Wirtschaft (Jena: Gustav Fischer, 1940; 2nd ed., 1944); W. H. Woglom (tr.), The Economics of Location (New Haven, Conn.: Yale University Press, 1954).

Hugh 0. Nourse, Regional Economics (New York: McGraw-Hill, 1968), Chapter 3.

John B. Parr, "Models of the Central Place System: A More General Approach," Urban. Studies, 15, 1 (February 1978), 35-49.

Harry W. Richardson, Regional Economics (New York: Praeger, 1969), Chapter 7.

APPENDIX 8-1

Trading-Area Boundaries Under Reilly’s Law see link

Assume two centers A and B located w miles apart, with center A having m times the population of center B. According to Reilly’s Law, the square of the distance from A to any point on the trading-area boundary will be m times the square of the distance from B to that point.

In this diagram, the locations are plotted with A at the origin and B on the horizontal axis at a distance w. A point X on the boundary is shown with coordinates x and y.

Reilly’s Law may now be stated as

y² + x²=m(y² + x² — 2xw + w²)                                                   (1)

y²(l — m) =—x²(1 — rn) — 2xmw + w²m                                     (2)

y² =w²m/(1— m) — 2xmw/(1 — rn) — x²                                     (3)

Let

z =x + mw/(1 — m)                                                                  (4)

Then

z²=x² + 2xmw/(1 — rn) + [mw/(1 — m)]²                                       (5)

-x²=-z² + 2xmw/(1 — m) + [mw/(1 — m)]² (                                     6)

Substituting in (3),

y²=rnw²/(1 — m) — 2xmw/(1 — m)— z²                                      (7)

                          +2xmw/(1 — m) + [mw/(1 — rn)]²

y²=[(mw² — m²w² + m²w²)/(1 — m)²]— z²                                    (8)

y² ± z²=mw²/(1 — m)²                                                                (9)

This is the equation of a circle with radius

The center of the circle is at z =0. Substituting in (4),

x=inw/(m—1)                                                                          (10)

The distance of the center of the circle from A is thus m/(m — 1) times the distance w from A to B. If m > 1 (that is, if A has the larger population), the center will then be to the right of B in the diagram, by a distance mw/(m — 1) — w =w/(m — 1).

In the special case of equal populations (m =1), there is no circle but a straight-line boundary, the perpendicular bisector of the line AB. Its equation is x =w/2.

APPENDIX 8-2

Concentration of U.S. Manufacturing Industries by Size Class of City (see section 8.4)

In section 8.4, a possible locational categorization of activities was suggested, according to whether the activity tends to locate predominantly (1) in large cities, (2) in small cities, or (3) without regard to city size. Some tabulations of Census data by the U.S. Department of Commerce provide the basis for such a categorization of all manufacturing industries on the rather detailed four-digit level of the Standard Industrial Classification. The data are from the Census of Manufactures, 1954.

The relative concentration of specific industries in specific size classes of cities is measured here by location quotients. A location quotient is a statistical measure of the degree to which any two quantitative characteristics are dissimilarly distributed between any two areas. Call the characteristics X and Y and the areas A and B, and let XA represent the amount of characteristic X in area A, and so on. Then the location quotient is (X_A/X_B) ÷ (Y_A/Y_B). An alternative way of expressing the same quotient is (X_A/Y_A) ÷ (X_B/Y_B). Both formulas give exactly the same result, since both are equal to (X_A Y_B)/(X_BY_A). The location quotient will be used a number of times later in this book.

In the case in hand, the areas are (A) a given size class of cities and (B) the United States as a whole, and the characteristics are (X) employment in a given manufacturing industry and (Y) employment in all manufacturing industries combined. Thus the location quotient for any given industry and size class of city is obtained by dividing the size class’s fraction of U.S. employment in the given industry (X_A/X_B)) by its fraction of U.S. employment in all industries (Y_A/Y_B).

The set of location quotients for any given industry gives a profile of that industry’s location pattern in relation to size class of city—for example, if the quotients are higher for the larger size classes, we can say that the industry in question tends to be more than proportionately represented in large cities.

Table 8-2-1 presents some illustrative findings. For each city size, a few industries have been picked out that most clearly show the specific concentration pattern indicated. It is interesting to note that all of the first group of industries (concentrated in the largest cities) appear also in the list of "external-economy industries" highly concentrated in New York (see Table 5-1). Table 8-2-1 includes also, at the end, a list of industries that seem to be located without regard to city size, since their location quotients for the different size classes all lie within a rather narrow range.

ENDNOTES

1. For convenience we shall often use the term "city" to mean any urban place, regardless of size.

2. The word "historical" is not meant to imply any lack of relevance to the future. The characteristic of the approach described here is that it considers changes (past and prospective) in specific cities. A pioneer American study along these lines was Adna F. Weber, The Growth of Cities in the Nineteenth Century, Columbia University Studies in History, Economics, and Public Law, 11 (New York: Macmillan, 1899; rev. ed., Ithaca, N.Y.: Cornell University Press, 1963). There are also countless histories of the origin and development of individual cities.

3. The self-reinforcing nature of urban growth, in a particular historical context, is especially well brought out in Allen R. Pred, The Spatial Dynamics of US. Urban-Industrial Growth, 1800-1914 (Cambridge, Mass.: MIT Press, 1966).

4. Wilbur R. Thompson, A Preface to Urban Economics (Baltimore: Johns Hopkins University Press, 1965), p. 24.

5. Walter Christaller, Die zentralen Orte in Süddeutschland (Jena: Gustav Fischer, 1933); C. W. Baskin (tr.), Central Places in Southern Germany (Englewood Cliffs N.J.: Prentice-Hall, 1966). An abstract of the theoretical parts of Christaller’s work appears in Brian J. L. Berry and Allen R. Pred, Central Place Studies: A Bibliography of Theory and Applications (Philadelphia: Regional Science Research Institute, 1961). See also August Lösch, Die räumliche Ordnung der Wirtschaft (Jena: Gustav Fischer, 1940); W. H. Woglom with the assistance of W. F. Stolper (trs.), The Economics of Location (New Haven, Conn.: Yale University Press, 1954). Berry’s definitive article, "Cities as Systems Within Systems of Cities" (which deals also with intracity location patterns), first appeared in Papers of the Regional Science Association. 13 (1964), 147-163.

6. In Lösch, Economics of Location, pp. 105 ff., the two activities were exemplified as agriculture and commercial brewing respectively. The brewers need grain and other farm products, and the farmers need beer.

7. In addition to the material in Section 4.2.2 concerning the market area of a spatial monopolist, the reader is referred to Appendix 4-1, where the relationship between pricing policies and conditions determining the existence and size of market areas is discussed in greater depth.

8. Martin Beckmann, Location Theory (New York: Random House, 1968), pp. 46-47.

Also, it should be noted that the requirement of "space-filling" shapes is not particularly descriptive of real-world situations. It implies that no buyer is excluded from purchasing a good because of transfer costs. In fact, transfer costs do make the delivered price of some goods prohibitively high in many locations.

9. It might appear obvious as well that products with lower transfer costs (per unit quantity and distance) would he produced in fewer centers, and distributed over larger market areas, than products with higher transfer costs. For reasons that will be shown later in this chapter, however, no such simple general statement about the relation of transfer costs to area size can be made.

10. John B. Parr, "Models of the Central Place System: A More General Approach," Urban Studies, 15, 1 (February 1978), 35-49.

11. See Brian J. L. Berry, "Research Frontiers in Urban Geography," in Philip M. Hauser and Leo F. Schnore (eds.), The Study of Urbanization (New York: Wiley, 1965), pp. 407-408. Berry’s article, in bibliographical notes appended on pp. 424-430, cites literature on both interurban and intraurban applications of central-place analysis.

12. The size distribution of cities within a large and relatively self-contained area has been found empirically to resemble a particular form described by the Rank-Size Rule. In its simplest formulation, this rule states that the size of a city is inversely proportional to its rank. Thus the second biggest city would be half the size of the biggest, the third biggest would he one-third the size of the biggest, the 500th biggest 1/500 the size of the biggest, and so on. This rule, originally wholly empirical, has been extensively tested, modified, and given some theoretical rationalization by Berry, Mills, and others. See Edwin S. Mills, Urban Economics (Glenview, Ill.: Scott, Foresman, 1972), Chapter 7; and Harry W. Richardson, "Theory of the Distribution of City Sizes: Review and Prospects," Regional Studies, 7,3 (September 1973), 239-251.

13. William J. Reilly, Methods for the Study of Retail Relationships, University of Texas Bulletin 2944 (Austin: University of Texas, 1929; reprinted, 1959); and The Law of Retail Gravitation (New York: Knickerbocker Press, 1931; 2nd ed., Pillsbury Publishers, 1953). Reilly’s analysis was mentioned above in introducing the "potential" or "gravity model" concept.

14. Ibid., p. 9.

15. If there are two cities w miles apart, one of which has a population m times that of the other, it can be shown that the market-area boundary according to Reilly’s Law is a circle of radius (w Ö m)(m — 1) with its center w /(m — 1) miles from the smaller city, in the direction away from the larger city. The larger city’s market area completely surrounds that of the smaller city. See Appendix 8-1 for derivation of these formulas, which were used in constructing Figure 8-4. The centers of the circles are marked by small crosses in the figure.

16. See James M. Henderson and Anne 0. Krueger, National Growth and Economic Changes in the Upper Midwest (Minneapolis: University of Minnesota Press, 1965), for the final general report on "‘the economic development phase of the Upper Midwest Economic Study (UMES) research program" and a listing of earlier reports. The results of the UMES Urban Research Program were published in a series of eight Urban Reports by John R. Borchert and others, listed ibid. p. 228. The material quoted in this chapter is taken from John R. Borchert and Russell B. Adams, Trade Centers and Trade Areas of the Upper Midwest, Upper Midwest Economics Study, Urban Report No. 3 (Minneapolis: September 1963).

17. Minneapolis-St. Paul was put in a class by itself in view of its unique role as the primary center for the entire region.

18. Large centers have multiple trade areas because they function at more than one level. For example, Fargo-Moorhead has successively larger trade areas at the complete shopping, secondary, and primary wholesale-retail levels." Ibid., p. 5.

19. The only metropolitan center within the Upper Midwest is Minneapolis-St. Paul, but such outside cities as Chicago, Portland, Seattle, Milwaukee, Des Moines, Omaha, and Denver received substantial proportions of the calls from nearby parts of the Upper Midwest. (See Figure 8-8.)

20. Ibid, p. 9.

21. The meat-packing industry in the United States is an interesting example of major locational shift. Initially highly dispersed, in the days when transport was costly and slow and refrigeration in transit impracticable, the industry developed massive concentration in the later nineteenth century at the larger Midwestern cities—on the basis of rail transport of both livestock and meat products and the economical utilization of by-products. But the ideal weights of transported input and output were never very different, and in the mid-twentieth century a trend toward decentralization set in. The giant stockyards and packing plants of Chicago, Omaha, Kansas City, St. Paul, and other old-time meat-packing centers were much curtailed during the 1950s and 1960s. Two major factors causing this locational shift were apparently (1) the shift of consumer markets toward the West Coast and the Gulf Coast and (2) the greater use of refrigerated transport of meat products by truck and air freight, without any corresponding improvement in the transportability of live animals. Facilitating the transfer of output tends, of course, to move an activity closer to its sources of inputs, and truck shipment permits more decentralization out of major terminal locations.

22. Flour milling and some other processing activities involving little if any loss of perishability or bulk and subject to considerable economies of scale are more often found in middlesized or even larger cities (such as Buffalo and Minneapolis).

23. John R. Borchert, The Urbanization of the Upper Midwest: 1930-1960, Upper Midwest Economic Study, Urban Report No. 2 (Minneapolis: February 1963), p. 19

24. U. S. Bureau of the Census, "Standard Metropolitan Statistical Areas and Consolidated Statistical Areas: 1980," Supplementary Reports, PC8O-S1-5 (Washington, D.C.: Government Printing Office, 1981), p. 2

25. William Alonso, "The Current Halt in the Metropolitan Phenomenon," in Charles L. Leven (ed.), The Mature Metropolis (Lexington, Mass.: Lexington Books, D.C. Heath, 1978), p. 28.

26. While Alonso’s remarks on this matter concern only population growth in metropolitan areas, Census data reveal that the relative change in metropolitan versus nonmetropolitan growth has also been affected by changes in the natural rate of population increase. The rate of population increase due to the excess of births over deaths has fallen less in non-metropolitan areas than in metropolitan areas in recent years. Thus some part of the observed turnaround is due to this factor, though as yet it is not possible to estimate its importance relative to that of other factors. See Larry Long and Diana DeAre, "Repopulating the Countryside: A 1980 Census Trend," Science, 217 (September 1982), p. 1112.

27. For a more advanced treatment of the effect of changes in such factors on equilibrium market areas, see Dennis R. Capozza and Kazem Attaran, "Pricing in Urban Areas Under Free Entry," Journal of Regional Science, 16, 2 (August 1976), 167-182.

28. U. S. Bureau of the Census, jointly with U.S. Department of Agriculture, Current Population Reports, Series P-27, No. 54, Farm Population of the United States: 1980 (Washington, D.C.: Government Printing Office, 1981).

29. U. S. Bureau of the Census, Current Population Reports, Series P-20, No. 363, Population Profile of the United States: 1980 (Washington, D.C.: Government Printing Office, 1981), p. 7.

30. Ibid., p. 7.

31. Larry H. Long and Diana DeAre, Migration to Nonmetropolitan Areas, Special Demographic Analysis, CDS 80-2, U.S. Bureau of the Census (Washington, D.C.: Government Printing Office, 1980), p. 1.

32. The Changing Demographic and Economic Structure of Nonmetropolitan Areas," International Regional Science Review, 2, 1 (Winter 1977), 123-142.

33. Where travel by retail buyers is involved, the benefit to the buyers is mainly a saving in time rather than money. To this extent, the transfer-cost reduction in itself does not increase effective market density and shrink trade areas as the income effect implies; the substitution effect dominates, and buyers respond to easier transfer by using more transfer (that is, traveling greater distances in search of cheaper or better goods and services).

The reader with some training in economics will recognize this conflict between substitution effect and income effect as something that quite generally occurs whenever an activity calls for two or more complementary inputs that are to some extent mutually substitutable. For example, if machinery becomes cheaper, there is an incentive to add machines and reduce employment; but at the same time, the cheaper machinery leads to a cheaper product and greater sales, which increases the demand for labor. The net effect on labor demand depends upon the terms of substitution between the two inputs and upon the elasticity of demand for the product.

34. For further discussion of transfer cost effects in the framework of simplified central-place models, see Walter Isard, Location and Space-Economy (Cambridge, Mass.: MIT Press, 1956), pp. 86-87; Hugh 0. Nourse, Regional Economics (New York: McGraw-Hill, 1968), pp. 215-216; Edgar M. Hoover, "Transport Costs and the Spacing of Central Places," Papers of the Regional Science Association, 25 (1970), 255-274; and Capozza and Attaran, "Pricing in Urban Areas."

35. For further reading on the causes and consequences of slow growth and decline in large metropolitan areas, see Charles L. Leven (ed.), The Mature Metropolis (Lexington, Mass.: Lexington Books, D. C. Heath, 1978).

36. See R. D. Norton and J. Bees, "The Product Cycle and the Spatial Decentralization of American Manufacturing," Regional Studies, 13, 2 (August 1979), 141-151.